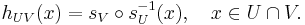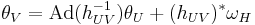Maurer–Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G. It was much used by Élie Cartan as a basic ingredient of his method of moving frames, and bears his name together with that of Ludwig Maurer.
As a one-form, the Maurer–Cartan form is peculiar in that it takes its values in the Lie algebra associated to the Lie group G. The Lie algebra is identified with the tangent space of G at the identity, denoted TeG. The Maurer–Cartan form ω is thus a one-form defined globally on G which is a linear mapping of the tangent space TgG at each g ∈ G into TeG. It is given as the pushforward of a vector in TgG along the left-translation in the group:
Contents |
Motivation and interpretation
A Lie group acts on itself by multiplication under the mapping
A question of importance to Cartan and his contemporaries was how to identify a principal homogeneous space of G. That is, a manifold P identical to the group G, but without a fixed choice of unit element. This motivation came, in part, from Felix Klein's Erlangen programme where one was interested in a notion of symmetry on a space, where the symmetries of the space were transformations forming a Lie group. The geometries of interest were homogeneous spaces G/H, but usually without a fixed choice of origin corresponding to the coset eH.
A principal homogeneous space of G is a manifold P abstractly characterized by having a free and transitive action of G on P. The Maurer–Cartan form[1] gives an appropriate infinitesimal characterization of the principal homogeneous space. It is a one-form defined on P satisfying an integrability condition known as the Maurer–Cartan equation. Using this integrability condition, it is possible to define the exponential map of the Lie algebra and in this way obtain, locally, a group action on P.
Construction of the Maurer–Cartan form
Intrinsic construction
Let 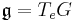 be the tangent space of a Lie group
be the tangent space of a Lie group  at the identity (its Lie algebra).
at the identity (its Lie algebra).  acts on itself by left translation
acts on itself by left translation
such that for a given 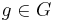 we have
we have
and this induces a map of the tangent bundle to itself
A left-invariant vector field is a section  of
of 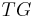 such that
such that
The Maurer–Cartan form  is a
is a  -valued one-form on
-valued one-form on  defined on vectors
defined on vectors 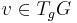 by the formula
by the formula
Extrinsic construction
If  is embedded in
is embedded in 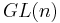 by a matrix valued mapping
by a matrix valued mapping 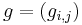 , then one can write
, then one can write  explicitly as
explicitly as
In this sense, the Maurer–Cartan form is always the left logarithmic derivative of the identity map of  .
.
Characterization as a connection
The Maurer–-Cartan form can also be characterized abstractly as a kind of principal connection. It is the unique g = TeG valued 1-form on G satisfying
where 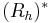 is the pullback of forms along the right-translation in the group and Ad(h−1) is the adjoint action on the Lie algebra.
is the pullback of forms along the right-translation in the group and Ad(h−1) is the adjoint action on the Lie algebra.
Properties
If  is a left-invariant vector field on
is a left-invariant vector field on  , then
, then 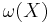 is constant on
is constant on  . Furthermore, if
. Furthermore, if  and
and  are both left-invariant, then
are both left-invariant, then
where the bracket on the left-hand side is the Lie bracket of vector fields, and the bracket on the right-hand side is the bracket on the Lie algebra  . (This may be used as the definition of the bracket on
. (This may be used as the definition of the bracket on  .) These facts may be used to establish an isomorphism of Lie algebras
.) These facts may be used to establish an isomorphism of Lie algebras
By the definition of the exterior derivative, if  and
and  are arbitrary vector fields then
are arbitrary vector fields then
Here ω(Y) is the  -valued function obtained by duality from pairing the one-form ω with the vector field Y, and X(ω(Y)) is the Lie derivative of this function along X. Similarly Y(ω(X)) is the Lie derivative along Y of the
-valued function obtained by duality from pairing the one-form ω with the vector field Y, and X(ω(Y)) is the Lie derivative of this function along X. Similarly Y(ω(X)) is the Lie derivative along Y of the  -valued function ω(X).
-valued function ω(X).
In particular, if  and
and  are left-invariant, then
are left-invariant, then
so
but the left-hand side is simply a 2-form, so the equation does not rely on the fact that  and
and  are left-invariant. The conclusion follows that the equation is true for any pair of vector fields
are left-invariant. The conclusion follows that the equation is true for any pair of vector fields  and
and  . This is known as the Maurer–Cartan equation. It is often written as
. This is known as the Maurer–Cartan equation. It is often written as
Maurer–Cartan frame
One can also view the Maurer–Cartan form as being constructed from a Maurer–Cartan frame. Let Ei be a basis of sections of TG consisting of left-invariant vector fields, and θj be the dual basis of sections of T*G such that θj(Ei) = δij, the Kronecker delta. Then Ei is a Maurer–Cartan frame, and θi is a Maurer–Cartan coframe.
Since Ei is left-invariant, applying the Maurer–Cartan form to it simply returns the value of Ei at the identity. Thus ω(Ei) = Ei(e) ∈ g. Thus, the Maurer–Cartan form can be written
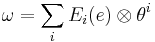 (1).
(1).
Suppose that the Lie brackets of the vector fields Ei are given by
The quantities cijk are constant, and called the structure constants of the Lie algebra (relative to the basis Ei). A simple calculation, using the definition of the exterior derivative d, yields
so that by duality
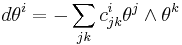 (2).
(2).
This equation is also often called the Maurer–Cartan equation. To relate it to the previous definition, which only involved the Maurer–Cartan form ω, take the exterior derivative of (1):
The frame components are given by
which establishes the equivalence of the two forms of the Maurer–Cartan equation.
Maurer–Cartan form on a homogeneous space
Maurer–Cartan forms play an important role in Cartan's method of moving frames. In this context, one may view the Maurer–Cartan form as a 1-form defined on the tautological principal bundle associated to a homogeneous space. If H is a closed subgroup of G, then G/H is a smooth manifold of dimension dim G - dim H. The quotient map G → G/H induces the structure of an H-principal bundle over G/H. The Maurer–Cartan form on the Lie group G yields a flat Cartan connection for this principal bundle. In particular, if H = {e}, then this Cartan connection is an ordinary connection form, and we have
which is the condition for the vanishing of the curvature.
In the method of moving frames, one sometimes considers a local section of the tautological bundle, say s : G/H → G. (If working on a submanifold of the homogeneous space, then s need only be a local section over the submanifold.) The pullback of the Maurer–Cartan form along s defines a non-degenerate g-valued 1-form θ = s*ω over the base. The Maurer–Cartan equation implies that
Morever, if sU and sV are a pair of local sections defined, respectively, over open sets U and V, then they are related by an element of H in each fibre of the bundle:
The differential of h gives a compatibility condition relating the two sections on the overlap region:
where ωH is the Maurer–Cartan form on the group H.
A system of non-degenerate g-valued 1-forms θU defined on open sets in a manifold M, satisfying the Maurer–Cartan structural equations and the compatibility conditions endows the manifold M locally with the structure of the homogeneous space G/H. In other words, there is locally a diffeomorphism of M into the homogeneous space, such that θU is the pullback of the Maurer–Cartan form along some section of the tautological bundle. This is a consequence of the existence of primitives of the Darboux derivative.
Notes
- ^ Introduced by Cartan (1904).
References
- Cartan, Élie (1904). "Sur la structure des groupes infinis de transformations". Annales scientifiques de l'É.N.S. 21: 153–206. http://archive.numdam.org/article/ASENS_1904_3_21__153_0.pdf.
- R. W. Sharpe (1996). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. Springer-Verlag, Berlin. ISBN 0-387-94732-9.
- Shlomo Sternberg (1964). "Chapter V, Lie Groups. Section 2, Invariant forms and the Lie algebra.". Lectures on differential geometry. Prentice-Hall. LCCN 64-7993.
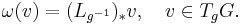
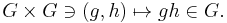
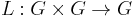
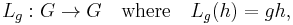
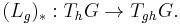
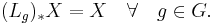
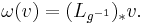
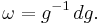
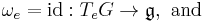
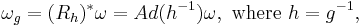
![\omega([X,Y])=[\omega(X),\omega(Y)]](/2012-wikipedia_en_all_nopic_01_2012/I/b2c43894d3ca110158373b22ff7c18e0.png)
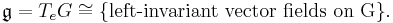
![d\omega(X,Y)=X(\omega(Y))-Y(\omega(X))-\omega([X,Y]).](/2012-wikipedia_en_all_nopic_01_2012/I/9328b5962aee30a19ed8978e972166d5.png)
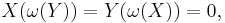
![d\omega(X,Y)%2B[\omega(X),\omega(Y)]=0](/2012-wikipedia_en_all_nopic_01_2012/I/cb89e1e323a0a55c6360fe31058441ec.png)
![d\omega %2B \frac{1}{2}[\omega,\omega]=0.](/2012-wikipedia_en_all_nopic_01_2012/I/5430a7a27b44081238d4527fe690d546.png)
![[E_i,E_j]=\sum_kc_{ij}^kE_k.](/2012-wikipedia_en_all_nopic_01_2012/I/a5a1808f28ddff6ba2344702167bbe1d.png)
![d\theta^i(E_j,E_k) = -\theta^i([E_j,E_k]) = -\sum_r c_{jk}^r\theta^i(E_r),](/2012-wikipedia_en_all_nopic_01_2012/I/2f191cca6587b28bbfd745c26adf7c47.png)
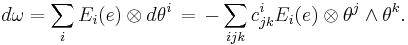
![d\omega(E_j,E_k) = -\sum_i c_{jk}^iE_i(e) = -[E_j(e),E_k(e)]=-[\omega(E_j),\omega(E_k)],](/2012-wikipedia_en_all_nopic_01_2012/I/af7d89b5eb606cb5fd6ec70c6366a751.png)
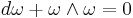
![d\theta %2B \frac{1}{2}[\theta,\theta]=0.](/2012-wikipedia_en_all_nopic_01_2012/I/ee3e6ea4ddeddcc571ba966914e6a84c.png)